Author: Will McCoy
This week we had our first meeting with our Engineering Liaisons at FPL. I’m very glad we were able to do this, because it allowed us to get some of our questions answered. However, an interesting constraint came out of this meeting which will radically change our final design; instead of having the $750-$1500 budget specified in the initial FPL Scope of Work, our sensor solution should end up costing less than $400. Additionally, our sensor should be able to log data about the vehicles it is tracking. These two factors put us in a bit of a pickle. Some baseline research indicates that edge processing systems cost at minimum $100, a camera array would cost at minimum $120, and that LiDARs cost at minimum $90. This leaves us with only $90 for the rest of the project, which may not be feasible. Additionally, there do not seem to be any LiDAR systems that a IP 67 rated and cost under $400. A cheaper solution would be to use 1D sensors, such as RaDAR or LiDAR sensors which only report distances. However, these would not be able to differentiate cars, and therefore would not give meaningful data to log. We will need to be very careful to reconcile these constraints in this project; hopefully it will be possible.
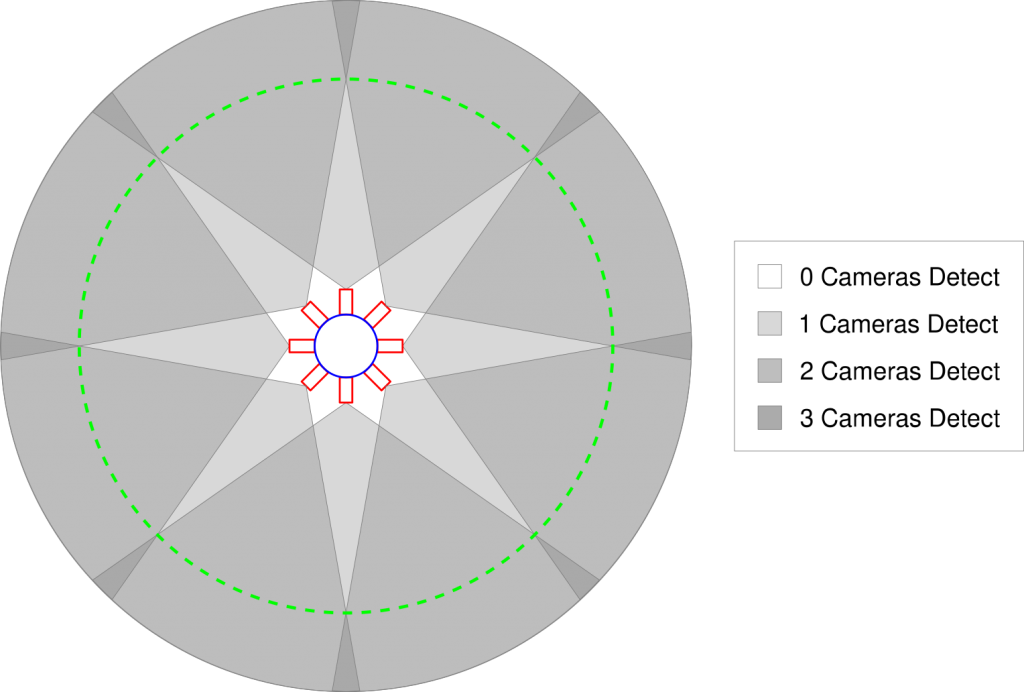
I also spent time this week researching computer vision, which is a field in computation dedicated to extracting information from images. To do this, I read the first chapter of Multiple View Geometry in Computer Vision, a textbook by Hartley and Zisserman. This chapter seemed to summarize the whole book, and thus there was a lot of information to go over. However, now that I know what I don’t know, I should be better able to fill in the gaps. One key takeaway was that, given knowledge about the configuration and properties of two cameras, a 2D point captured by both cameras can be transformed back into a 3D point in the original scene. This principle, called binocular vision, is how the human eye works. Using this principle, I came up with a preliminary design of a camera array, which shows how all points a certain distance from the array can be identified in 3D space (relative to the camera array). This can be seen below.